Machine Learning-Standard Deviation
Độ lệch chuẩn Standard Deviation là gì ?
Standard Deviation có nghĩa là độ lệch chuẩn hay còn gọi là độ lệch tiêu chuẩn.
Độ lệch chuẩn Standard Deviation là một đại lượng dùng để đo mức độ phân tán, dàn trải của một tập dữ liệu.
Độ lệch chuẩn thấp có nghĩa là hầu hết các giá trị trong tập dữ liệu gần với giá trị trung bình.
Độ lệch chuẩn cao có nghĩa là hầu hết các giá trị trong tập dữ liệu dàn trải, phân tán trên một phạm vi rộng so với giá trị trung bình.
Cách tính độ lệch chuẩn Standard Deviation trong toán học.
Độ lệch chuẩn được tính bằng cách lấy căn bậc hai của phương sai.
Công thức tính độ lệch tiêu chuẩn như sau:
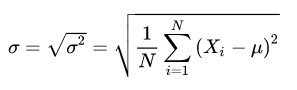
σ : là độ lệch chuẩn
σ2 : là phương sai
N: là số phần tử của tập dữ liệu
Xi là phần tử thứ i
μ: là trung bình cộng của tập dữ liệu.
Ví dụ: Bài toán tìm mức độ phân tán, dàn trải điểm môn Tiếng Anh của 15 sinh viên.
points_English = [100,99,82,87,81,82,96,87,94,78,71,85,82,83,82]
Để tìm mức độ phân tán, dàn trải dữ liệu có nghĩa là chúng ta cần tìm độ lệch chuẩn.
Các bước tính độ lệch tiêu chuẩn :
Bước 1: Tính giá trị trung bình
(100+99+82+87+81+82+96+87+94+78+71+85+82+83+82) / 15 = 85.93
Bước 2: Tính độ lệch của từng giá trị với giá trị trung bình
100 - 85.93 = 14.07
99 - 85.93 = 13.07
82 - 85.93 = -3.93
87 - 85.93 = 1.07
81 - 85.93 = -4.93
82 - 85.93 = -3.93
96 - 85.93 = 10.07
87 - 85.93 = 1.07
94 - 85.93 = 8.07
78 - 85.93 = -7.93
71 - 85.93 = -14.93
85 - 85.93 = -0.93
82 - 85.93 = -3.93
83 - 85.93 = -2.93
82 - 85.93 = -3.93
Bước 3: Tính phương sai
Phương sai là trung bình cộng của các bình phương độ lệch.
((14.07)2 + (13.07)2 + (-3.93)2 + (1.07)2 + (-4.93)2 + (-3.93)2 + (10.07)2 + (1.07)2 + (8.07)2 + (-7.93)2 + (-14.94)2 + (-0.93)2 + (-3.93)2 + (-2.93)2 + (-3.93)2)/15 = 61.26
Bước 4: Tính độ lệch chuẩn.
Độ lệch chuẩn bằng căn bậc hai của phương sai.
√61.26 = 7.82
Đó là cách tính độ lêch chuẩn trong toán học.Tuy nhiên trong Numpy Python có phương thức std() để tính độ lệch chuẩn rất dễ dàng và đơn giản.
Cách tính độ lệch chuẩn sử dụng phương thức std() trong python.
Sử dụng phương thức std() trong thư viện Numpy của Python để tính độ lệch chuẩn.
Ví dụ
import numpy as np
# Danh sách điểm môn tiếng anh của 15 sinh viên:
points_English = [100,99,82,87,81,82,96,87,94,78,71,85,82,83,82]
# Tính độ lệch chuẩn bằng phương thức std() trong python.
std1 = np.std(points_English)
print("Do lech chuan la:", std1)
Kết quả :
Do lech chuan la: 7.82
Sử dụng phương thức var() trong thư viện Numpy để tính phương sai.
Ví dụ
import numpy as np
# Danh sách điểm môn tiếng anh của 15 sinh viên:
points_English = [100,99,82,87,81,82,96,87,94,78,71,85,82,83,82]
# Tính phương sai sử dụng phương thức var() trong numpy của python.
var_phuongsai = np.var(points_English)
print("Phuong sai la:", var_phuongsai)
Kết quả :
Phuong sai la: 61.26
Ý nghĩa của độ lệch chuẩn Standard Deviation
Độ lệch chuẩn thường được dùng trong thống kê, nó đo tính biến động, chênh lệch của các giá trị ở những thời điểm khác nhau so với giá trị trung bình.
Thuật toán độ lệch chuẩn (Standard Deviation) và phương sai (Variance) là thường sử dụng trong Machine Learning, vì vậy bạn cần nắm chắc và hiểu rõ khái niệm này để phát triển cho các ứng dụng về machine learning sau này.
