Machine Learning - Thuật toán Polynomial Regression
Polynomial Regression là gì?
Polynomial Regression là thuật toán hồi quy đa thức, nó giống như thuật toán hồi quy tuyến tính, sử dụng mối quan hệ giữa các biến độc lập x và biến phụ thuộc y được biểu diễn dưới dạng đa thức bậc n, để tìm cách tốt nhất vẽ một đường qua các điểm dữ liệu sao cho tối ưu và phù hợp nhất. Polynomial Regression là một thuật toán trong machine learning, nó được dùng cho các bài toán về dự đoán, dự báo (prediction).
Dạng tổng quát của Polynomial Regression như sau:
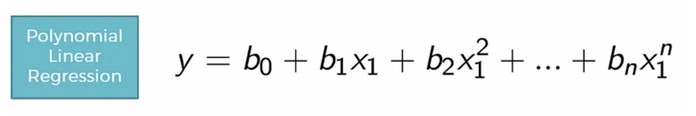
Một số dạng thường gặp của Polynomial Regression:
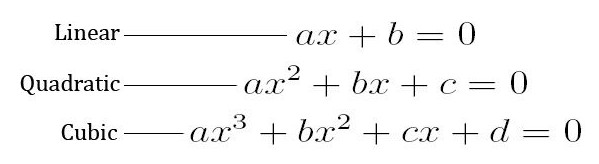
Biểu đồ:
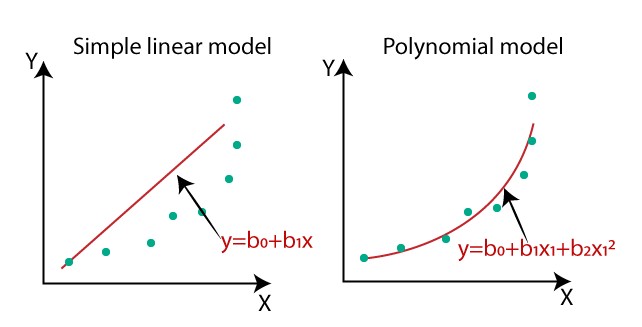
Tại sao cần Polynomial Regression ?
Trong trường hợp các điểm dữ liệu không phù hợp với hồi quy tuyến tính Linear Regression.(Các điểm không phân bố dưới dạng đường thẳng).Các điểm phân bố, phân tán dưới dạng đường cong, do đó thuật toán hồi quy tuyến tính Linear Regression không phù hợp vì vậy bạn phải cần sử dụng Polynomial Regression để tối ưu hơn.
Thuật toán Polynomial Regression trong machine learning với Python.
Ví dụ: Bài toán đăng ký tốc độ xe ô tô theo thời gian trong ngày (giờ) qua trạm thu phí.
Giả sử trong trong một ngày có 18 chiếc ô tô qua trạm thu phí và các ô tô này được đăng ký trong các thời gian trong ngày như sau:
Thời gian ô tô đăng ký qua trạm được thể hiện tập dữ liệu x như sau:
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
Tốc độ của ô tô tương ứng với giờ đã đăng ký qua trạm thu phí là y.
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]
Hãy tìm tốc độ mà thời gian ô tô đăng ký qua trạm lúc 17 giờ ?
Để giải quyết bài toán này, trước tiên chúng ta xem sự phân bố, phân tán của tập dữ liệu ở trên thông qua biểu đồ phân tán scatter.
Ví dụ
import matplotlib.pyplot as plt
# Thời gian đăng ký qua trạm thu phí
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
# Tốc độ cua xe tương ứng với thời gian qua trạm.
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]
plt.scatter(x, y)
plt.show()
Kết quả như sau:
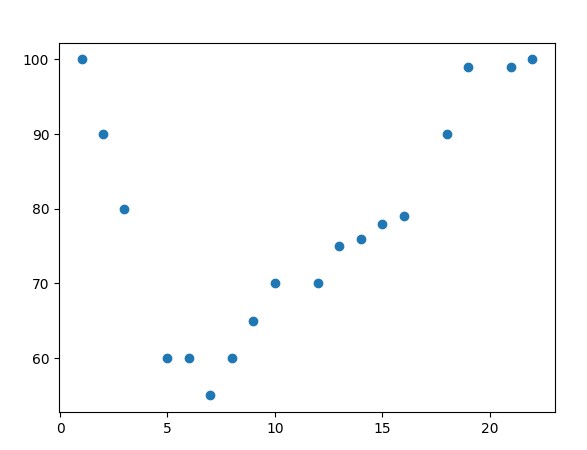
Quan sát qua biểu biểu đồ trên chúng ta thấy tập hợp các điểm dữ liệu phân bố có dạng đường cong, do đó chúng ta nhận thấy thuật toán Polynomial Regression phù hợp với bài toán này hơn so với thuật toán Linear Regression.
Thuật toán Polynomial Regression trong machine learning với Numpy.
Ví dụ
import numpy
import matplotlib.pyplot as plt
# Thời gian đăng ký qua trạm thu phí
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
# Tốc độ cua xe tương ứng với thời gian qua trạm.
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))
myline = numpy.linspace(1, 22, 100)
plt.scatter(x, y)
plt.plot(myline, mymodel(myline))
plt.show()
Kể quả thể hiện trên biểu đồ sau:
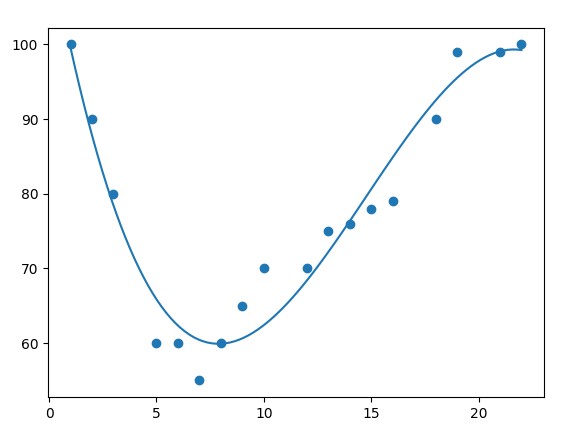
Thuật toán Polynomial Regression trong machine learning với sklearn.
Thư viện sklearn có các phương thức hỗ trợ cho việc tính toán và dự đoán.
Sử dụng hàm R-Squared để đo mối qua hệ giữa các biến độc lập x và biến phụ thuộc y.
Giá trị hàm R-Squared nằm trong khoảng từ 0 đến 1. Trong đó 0 có nghĩa là không có mối quan hệ và 1 có nghĩa là 100% có liên quan.
Trong Python và module sklearn sẽ tính toán giá trị này cho bạn.Bạn chỉ cần truyên dữ liệu đầu vào bằng các mảng dữ liệu x và y.
Bây giờ chúng ta qua trở lại với bài toán đăng ký tốc độ xe ô tô theo thời gian trong ngày.Chúng ta sẽ đánh giá và dự đoán tốc độ của xe đăng ký lúc 17h bằng thuật toán R-Squared trong thư viện sklearn.
Ví dụ
import numpy
from sklearn.metrics import r2_score
x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]
mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))
# Đánh giá mô hình bằng R-Squared
print(r2_score(y, mymodel(x)))
# Dự đoán tốc độ lúc 17h
speed = mymodel(17)
print(speed)
Kết quả :
0.9432150416451026
88.87331269698001
Chúng ta thấy kết quả đánh giá mô hình r2_score=0.94.Kết quả 0,94 cho thấy có một mối quan hệ rất tốt và chúng ta có thể sử dụng hồi quy đa thức trong các dự đoán trong tương lai.
Kết quả dự đoán tốc độ đăng ký lúc 17h là: 88.87 .
