Machine Learning - Normal Distribution

Phân phối chuẩn Normal Distribution là gì?

Normal Distribution có nghĩa là phân phối chuẩn. Nó là một phân phối xác suất quan trọng được sử dụng phổ biến nhất trong thống kê.

Phân phối chuẩn Normal Distribution còn được gọi là phân phối Gaussian hoặc đường cong hình chuông.

Đặc điểm của phân phối chuẩn Normal Distribution.

Phân phối chuẩn Normal Distribution có hình dạng đường cong hình chuông.

Phân phối chuẩn Normal Distribution là được mô tả bởi giá trị trung bình Mean (μ) và độ lệch chuẩn Standard Deviation (σ).

Giá trị Trung vị Median và Trung bình Mean là bằng nhau.

Giá trị trung bình Mean mô tả ở vị trí trung tâm của phân phối chuẩn.

Độ lệch chuẩn Standard Deviations mô tả mức độ dàn trải, trải rộng của phân phối chuẩn Normal Distribution.

Phân phối đối xứng, có nghĩa là nó giảm cùng một lượng ở bên trái và bên phải của trung tâm.

Khu vực dưới đường cong của phân phối chuẩn Normal Distribution thể hiện xác suất đối với dữ liệu. Khu vực bên dưới toàn bộ đường cong bằng 1 hoặc 100%.

Quy tắc thực nghiệm trong phân phối chuẩn.

Quy tắc thực nghiệm hoặc quy tắc 68-95-99.7, cho bạn biết phần lớn các giá trị của bạn nằm ở đâu trong phân phối chuẩn:

     Khoảng 68% giá trị nằm trong 1 độ lệch chuẩn so với giá trị trung bình.

     Khoảng 95% giá trị nằm trong khoảng 2 độ lệch chuẩn so với giá trị trung bình.

     Khoảng 99,7% giá trị nằm trong khoảng 3 độ lệch chuẩn so với giá trị trung bình.

Ví dụ: Sử dụng quy tắc thực nghiệm trong phân phối chuẩn Normal Distrinution.
Bạn thu thập điểm SAT của học sinh trong một khóa luyện thi mới. Dữ liệu tuân theo phân phối chuẩn với điểm trung bình (μ) là 1150 và độ lệch chuẩn (σ) là 150.

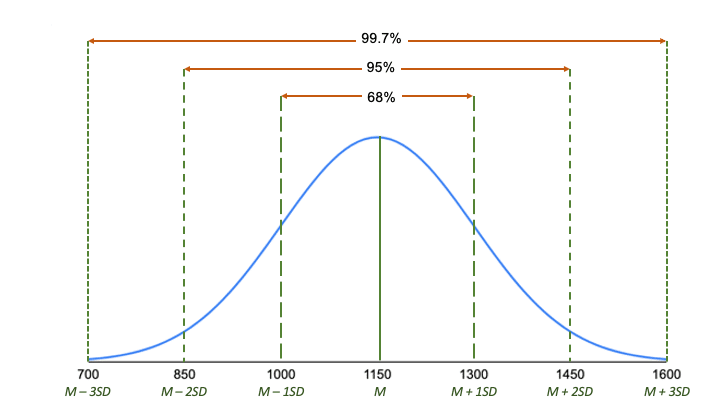
 Quy tắc thực nghiệm là một cách nhanh chóng để có cái nhìn tổng quan về dữ liệu của bạn và kiểm tra bất kỳ giá trị ngoại lệ hoặc giá trị  nào không tuân theo mẫu này.

Quan sát biểu đồ phân phổi chuẩn Normal Distribution ở bên trên cho chung ta thấy:

- Khoảng 68% điểm nằm trong khoảng 1.000 đến 1.300, 1 độ lệch chuẩn trên và dưới mức trung bình.
- Khoảng 95% điểm số nằm trong khoảng từ 850 đến 1,450, 2 độ lệch chuẩn trên và dưới mức trung bình.
- Khoảng 99,7% điểm số nằm trong khoảng từ 700 đến 1.600, 3 độ lệch chuẩn trên và dưới mức trung bình.

Cách tính phân phối chuẩn Normal Distribution trong toán học và thống kê.

Trong toán học và thống kê, phân phối chuẩn Normal Distribution sử dụng công thức sau:

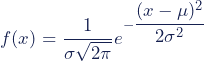
    f(x) = probability : Xác Suất
    x = value of the variable : Giá trị của biến
    μ = mean : Giá trị trung bình
    σ = standard deviation : Độ lệch chuẩn
    σ2 = variance : Phương sai

Cách tính Phân phối dữ liệu chuẩn Normal Distribution trong Machine Learning

Trong lập trình Machine learning sử dụng phương thức : numpy.random.normal() để tính phân phối chuẩn.

Ví dụ về phân phối chuẩn Normal Distribution trong lập trình machine learning như sau:

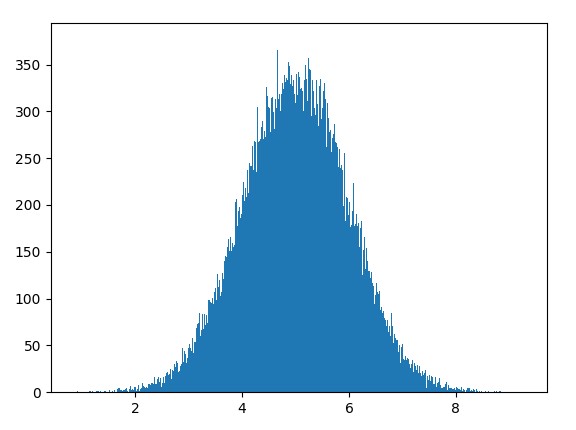
Giải thích biểu đồ:

Quan sát biểu đồ trên chúng ta thấy biểu đồ có hình dạng giống như hình chuông (bell), do đó nó được gọi là đường cong hình chuông (bell curves).

Biểu đồ trên thể hiện phân phối dữ liệu của 100000 giá trị với giá trị trung bình là 5.0 và độ lệch chuẩn là 1.0

Biểu đồ trên được vẽ bởi 1000 bars (1000 thanh hoặc cột).

Nhìn vào biểu đồ trên cho chúng ta thấy các giá trị hầu hết chủ yếu nằm trong khoảng từ 4.0 đến 6.0 với giá trị xấp xỉ gần bằng 5.0.

Ứng dụng của phân phối chuẩn Normal Distribution trong thực tế.

Phân phối chuẩn Normal Distributon được ứng dụng trong các bài toán thống kê.

Ví dụ 1: Bài toán về cân nặng của trẻ sơ sinh (Birthweight of Babies).

Ví dụ 2: Bài toán về  chiều cao (Height of Males).

Ví dụ 3: Bài toán về Kích thước giầy (Shoe Sizes).

Ví dụ 4: Bài toán về Tuổi nghỉ hưu trung bình của các cầu thủ NFL (Average NFL Player Retirement Age).

Ví dụ 5: Bài toán về mức độ hài lòng công việc.

Ví dụ 6: Bài toán về điểm ACT (ACT Scores).

Ví dụ 7: Bài toán về huyết áp (Blood Pressure).

Ví dụ 8: Bài toán về khả năng đọc.

Hiểu các thuộc tính của phân phối chuẩn bạn có thể sử dụng thống kê suy luận để so sánh các nhóm khác nhau và đưa ra ước tính bằng cách sử dụng mẫu.