Machine Learning-Thuật toán Simple Linear Regression
Simple Linear Regression là gì?
Simple Linear Regression là thuật toán hồi quy tuyến tính trong machine learning, nó được dùng cho các bài toán về dự đoán, dự báo (prediction).
Hồi quy tuyến tính là một phương pháp thống kê để thiết lập mối quan hệ giữa biến phụ thuộc (y) và biến độc lập (x).
Như chúng ta đã biết trong machine learning có 2 bài toán cơ bản đó là bài toán học có giám sát (supervised learning) và bài toán hoạc không giám sát (unsupervised learning).Thuật toán Linear Regression là một thuật toán thuộc bài toán học có giám sát (supervised learning).
Học có giám sát có nghĩa là bài toán được xây dựng dựa trên dữ liệu có nhãn để tìm ra mối quan hệ giữa biến đầu vào (biến độc lập) với biến đầu ra (biến phụ thuộc hoặc biến mục tiêu).
Học có giám sát được phân loại thành bài toán dự báo (prediction) và bài toán phân loại (classification).
Bài toán dự báo (prediction) là bài toán được áp dụng trên biến đầu ra liên tục, bài toán này sẽ trả lời cho câu hỏi giá trị của một quan sát đươc dự đoán là bằng bao nhiêu ?
Ứng dụng của thuật toán hồi quy tuyến tính Linear Regression.
Thuật toán hồi quy tuyến tính Linear Regression có rất nhiều ứng dụng trong thực tiễn và là một trong những mô hình đặc biệt quan trọng trong machine learning. Chúng ta sẽ không thể kể hết được ứng dụng của nó trong một vài dòng. Nhưng chúng ta có thể xét đến một vài ví dụ tiêu biểu và gần gũi với mọi người, chẳng hạn như các bạn thường được nghe các dự báo trên truyền hình về chỉ số lạm phát, tốc độ tăng trưởng GDP của quốc gia hay dự báo về nhu cầu thị trường của một doanh nghiệp để chuẩn bị kế hoạch sản suất kinh doanh. Trong tài chính chúng ta có thể dự báo giá chứng khoán, dự báo dư nợ xấu và các chỉ số tài chính dựa trên hồi quy tuyến tính.Ngoài ra còn được ứng dụng trong rất nhiều lĩnh vực khác như dự báo lương trong công ty, dự báo giá nhà trong lĩnh vực bất động sản, dự báo giá cước xe taxi...
Hầu hết các bài toán dự báo liên quan tới biến mục tiêu liên tục thì đều có thể sử dụng hồi quy tuyến tính để dự báo.
Trong bài này chúng tôi sẽ chia sẻ và giúp các bạn hiểu được về thuật toán Linear Regression trong toán học và ứng dụng của thuật toán này trong lập trình machine learning.
Thuật toán hồi quy tuyến tính đơn biến Simple Linear Regression trong toán học.
Trường hợp đơn giản của thuật toán hồi quy tuyên tính Linear Regression có dạng như sau:
y = ax + b
Với a,b là các hằng số, a#0.
y : Biến phụ thuộc, biến mục tiêu
x : Biến độc lập
b : Hằng số
a : Hệ số mối quan hệ giữa x và y.
Do có một biến đầu vào (biến x) nên nó gọi là phương trình hồi quy tuyến tính đơn biến.Dạng bài toán này chúng ta đã gặp khi còn học hồi cấp 3.
Trong không gian 2 chiều quan hệ giữ x và y thể hiện là một đường thẳng.
Bây giờ chúng ta sẽ đi tìm hiểu về bài toán hồi quy tuyến tính Simple Linear Regression .
Giả sử chúng ta xét phương trình hồi quy đơn biến với n quan sát có biến phụ thuộc là
y = {y1,y2,y3…yn} và biến đầu vào x = {x1,x2,x3…xn}.Véc tơ w = (w0,w1) với w0,w1 lần lượt là hằng số và hệ số ước lượng.
Từ dữ liệu đầu vào chúng ta biểu diễn bằng phương trình hồi quy tuyến tính như sau:
yi^ = f(xi) = w0 + w1*xi
Trong đó (xi, yi) là mô tả cho các điểm dữ liệu thứ i.
Mục tiêu của chúng ta là đi tìm véc tơ w hoặc các giá trị w0,w1 sao cho sai số giữa giá trị dự báo và thực tế là nhỏ nhất. Tức là tối thiểu hoá hàm mất mát MSE (Mean Square Error).
Hàm mất mát L(w) được tính như sau:
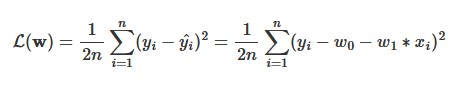
L(w) là hàm mất mát, là một hàm theo w0,w1. Bây giờ nhiệm vụ của chúng ta là cần tìm các giá trị w0,w1.Chúng ta có thể tìm cực trị của phương trình trên dựa vào đạo hàm theo w0,w1 như sau:
Đạo hàm theo w0:
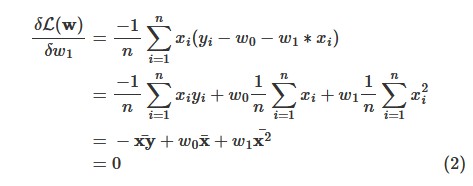
Đạo hàm theo w1:
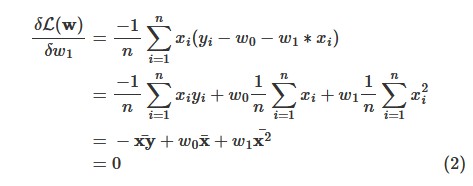
Giải phương trình trên ta được nghiệm w0,w1 như sau: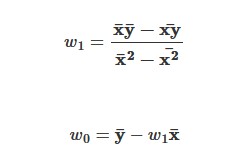
Trên đây là cách giải bài toán hồi quy tuyến tính trong toán học, vậy để áp dụng thuật toán này vào trong lập trình machine learning cho các bài toán trong thực tiễn như thế nào? Bài toán dưới đây chúng tôi sẽ giúp bạn hiểu được ứng dụng của nó.
Ví dụ: Chúng ta sẽ dự đoán giá nhà dựa vào diện tích.
Giả sử chúng ta có 15 căn hộ với diện tích (đơn vị m2) như sau:
x = [60,65,70,72,75,80,82,85,88,90,95,100,120,150,160]
Với mức giá (trăm triệu vnđ) tương ứng cho các căn hộ có diện tích ở trên là:
y = [500,550,600,620,700,720,740,800,810,850,880,900,920,960,980]
Làm thế nào để dự đoán giá nhà có diện tích 110 m2?
Để giải quyết bài toán này chúng ta sử dụng thuật toán hồi quy tuyến tính đơn biến Simple Linear Regression trong machine learning.
Thuật toán hồi quy tuyến tính đơn biến Simple Linear Regression trong Machine Learning.
Ví dụ
import matplotlib.pyplot as plt
import numpy as np
# Diện tích nhà (area)
x = np.array([[60,65,70,72,75,80,82,85,88,90,95,100,120,150,160]]).T
# Giá nhà (price)
y = np.array([[500,550,600,620,700,720,740,800,810,850,880,900,920,960,980]]).T
# Biểu diễn trực quan dữ liệu bằng biểu đồ (Visualize data)
def _plot(x, y, title="", xlabel="", ylabel=""):
plt.figure(figsize=(14, 8))
plt.plot(x, y, 'r-o', label="price")
x_min = np.min(x)
x_max = np.max(x)
y_min = np.min(y)
y_max = np.max(y)
# mean price
ybar = np.mean(y)
plt.axhline(ybar, linestyle='--', linewidth=4, label="mean")
plt.axis([x_min*0.95, x_max*1.05, y_min*0.95, y_max*1.05])
plt.xlabel(xlabel, fontsize=16)
plt.ylabel(ylabel, fontsize=16)
plt.text(x_min, ybar*1.01, "mean", fontsize=16)
plt.legend(fontsize=15)
plt.title(title, fontsize=20)
plt.show()
_plot(x, y,
title='Giá nhà theo diện tích',
xlabel='Diện tích (m2)',
ylabel='Giá nhà (Trăm triệu VND)')
# Tính trung bình
xbar = np.mean(x)
ybar = np.mean(y)
x2bar = np.mean(x**2)
xybar = np.mean(x*y)
# Tính w0, w1
w1 = (xbar*ybar-xybar)/(xbar**2-(x2bar))
w0 = ybar-w1*xbar
xi=110
print('w1: ', w1)
print('w0: ', w0)
print('Diện tích: xi =',xi)
yi=w0 + w1*110
print("Giá nhà 110 m2 là: yi= ", yi )
Kết quả :
w1: 4.452892069171154
w0: 355.4382826475835
Diện tích: xi = 110
Giá nhà 110 m2 là: yi= 845.2564102564105
Thuật toán Simple Linear Regression sử dụng thư viện Scikit-learn trong machine learning.
Scikit-learn (Sklearn) là thư viện mạnh mẽ, quan trọng được dùng cho các thuật toán machine learning, nó được viết bằng ngôn ngữ Python.
Ví dụ
from sklearn import datasets, linear_model
import numpy as np
import matplotlib.pyplot as plt
# diện tích area
x = np.array([[60,65,70,72,75,80,82,85,88,90,95,100,120,150,160]]).T
# Giá nhà price
y = np.array([[500,550,600,620,700,720,740,800,810,850,880,900,920,960,980]]).T
# Biểu diễn trực quan dữ liệu bằng biểu đồ (Visualize data)
plt.scatter(x, y);
plt.xlabel('Diện tích (m2)')
plt.ylabel('Giá tiền (Trăm triệu vnđ)')
plt.title('Giá nhà theo diện tích')
plt.show()
# Tạo Xbar
one = np.ones((x.shape[0], 1))
Xbar = np.concatenate((one, x), axis = 1)
# Tối ưu hóa bằng thuật toán Linear Regression
regr = linear_model.LinearRegression(fit_intercept=False)
# Huấn luyện
regr.fit(Xbar, y)
# Kết quả
w = regr.coef_
print( 'Tìm w sử dụng scikit-learn : ', w )
w0=w[0][0]
w1=w[0][1]
xi=110
yi = w0 + w1*xi
print("w0:",w0)
print("w1:",w1)
print("Diện tích:",xi)
print("Giá nhà 110 m2 là: yi= ", yi)
# Biểu diễn trực quan dữ liệu bằng biểu đồ (Visualize data)
plt.scatter(x, y);
plt.plot(x, w[0][1] * x + w[0][0], linestyle='solid', color='red')
plt.xlabel('Diện tích (m2)')
plt.ylabel('Giá tiền (Trăm triệu vnđ)')
plt.title('Giá nhà theo diện tích')
plt.show()
Kết quả :
Tìm w sử dụng scikit-learn : [[355.43828265 4.45289207]]
w0: 355.4382826475848
w1: 4.452892069171137
Diện tích: xi = 110
Giá nhà 110 m2 là: yi= 845.2564102564098
Kết quả ở bài toán trên được biểu diễn bằng biểu đồ, đồ thị như hình dưới đây:
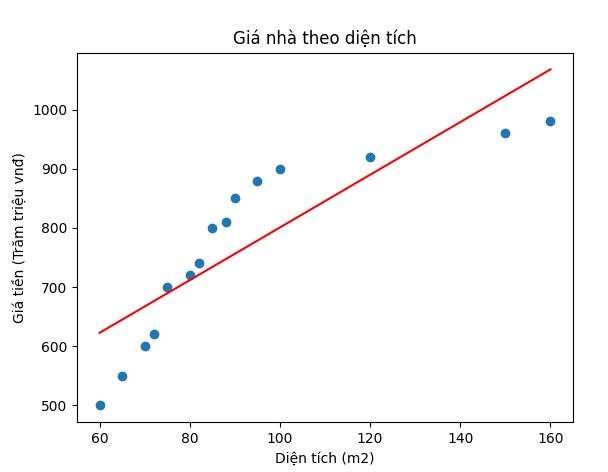
- Các điểm hình tròn màu xanh biểu diễn các điểm có giá trị (xi,yi) tương ứng với diện tích và giá nhà.
- Các điểm nằm trên đường thẳng màu đỏ là kết quả dự đoán, dự báo.
- Kết quả dự đoán của ngôi nhà có diện tích 110 m2 có giá là 845 triệu.
